Redes Neurais Profundas | Prof. Dr. Guilherme Souza Rodrigues
Considere um processo gerador de dados da forma \[\begin{align*} Y & \sim N(\mu, \sigma^2=1) \\ \mu & = |X_1^3 - 30 \text{sen} (X_2) + 10| \\ X_j & \sim \text{Uniforme}(-3, 3), \quad j=1, 2. \end{align*}\]
Neste modelo (que iremos considerar como o “modelo real”), a esperança condicional de \(Y\) é dada por \(E(Y|X_1, X_2) = |X_1^3 - 30 \text{sen} (X_2) + 10|\). A superfície tridimensional \((E(Y|X_1, X_2), X_1, X_2)\) está representada em duas dimensões cartesianas na Figura 1.
O código a seguir simula \(m=100.000\) observações desse processo.
### Gerando dados "observados"
set.seed(22025)
m.obs <- 100000
dados <- tibble(x1.obs=runif(m.obs, -3, 3),
x2.obs=runif(m.obs, -3, 3)) %>%
mutate(mu=abs(x1.obs^3 - 30*sin(x2.obs) + 10),
y=rnorm(m.obs, mean=mu, sd=1))Nesta lista estamos interessados em estimar o modelo acima usando uma rede neural simples, ajustada sobre os dados simulados. Precisamente, queremos construir uma rede neural com apenas uma camada escondida contendo dois neurônios.
Matematicamente, a rede é descrita pelas seguintes equações: \[\begin{align*} f_{0, 1} & = x_1 w1 + x_2 w2 + b_1 \\ f_{0, 2} & = x_1 w3 + x_2 w4 + b_2 \\ h_{1, 1} & = a(f_{0, 1}) \\ h_{1, 2} & = a(f_{0, 2}) \\ f_{1, 1} & = h_{1, 1} w_5 + h_{1, 2} w_6 + b_3 \\ \hat{y} & = h_{2, 1} = f_{1, 1}, \end{align*}\] onde \(a(x) = \frac{1}{1+e^{-x}}\) representa a função de ativação logística (sigmoide).
Adotaremos como função de perda o erro quadrático médio, expresso por \[ J(\boldsymbol{\phi}) = \frac{1}{m} \sum_{i=1}^m L(f(x_{1i}, x_{2i}; \boldsymbol{\phi}), y_i) = \frac{1}{m} \sum_{i=1}^m (y_i - \hat{y}_i)^2, \] onde \(x_{ji}\) representa a j-ésima covariável (feature) da i-ésima observação, \(\boldsymbol{\phi} = (w_1, \ldots, w_6, b_1, b_2, b_3)\) é o vetor de pesos e viéses (parâmetros) e, pela definição da rede, \[f(x_{1i}, x_{2i}; \boldsymbol{\phi})=\hat{y}_i=a(x_{1i} w_1 + x_{2i} w_3 + b_1) w_5 + a(x_{1i} w_2 + x_{2i} w_4 + b_2) w_6 + b_3.\] Uma representação gráfica da rede está apresentada na Figura 2.
Em notação matricial, a rede neural pode ser descrita por \[\begin{align*} \boldsymbol{f}_0 & = \boldsymbol{\Omega}_0 \boldsymbol{x} + \boldsymbol{\beta}_0 \\ \boldsymbol{h}_1 & = \boldsymbol{a}(\boldsymbol{f}_0) \\ f_1 & = \boldsymbol{\Omega}_1 \boldsymbol{h}_1 + \boldsymbol{\beta}_1 \\ \hat{y} & = h_2 = f_1, \end{align*}\] onde \[\begin{equation*} \boldsymbol{x} = \boldsymbol{h}_0 = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}, \; \boldsymbol{\Omega}_0 = \begin{pmatrix} w_1 & w_2 \\ w_3 & w_4 \end{pmatrix}, \; \boldsymbol{\beta}_0 = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}, \; \boldsymbol{f}_0 = \begin{pmatrix} f_{0, 1} \\ f_{0, 2} \end{pmatrix}, \; \boldsymbol{h}_1 = \begin{pmatrix} h_{1, 1} \\ h_{1, 2} \end{pmatrix}, \; \boldsymbol{\Omega}_1 = \begin{pmatrix} w_5 & w_6 \end{pmatrix}, \; \beta_1 = b_3 \quad \text{e} \end{equation*}\] \[\begin{equation*} \boldsymbol{\Phi} = \{\boldsymbol{\Omega} = \{\boldsymbol{\Omega}_0, \boldsymbol{\Omega}_1\}, \boldsymbol{\beta} = \{\boldsymbol{\beta}_0, \beta_1\}\}. \end{equation*}\]
Figura 1: Gráfico da superfície do valor esperado da variável resposta \(Y\) em função das variáveis de entrada \(X_1\) e \(X_2\).
### Figura 1: Gerando o gráfico da superfície
n <- 100
x1 <- seq(-3, 3, length.out=n)
x2 <- seq(-3, 3, length.out=n)
dados.grid <- as_tibble(expand.grid(x1, x2)) %>%
rename_all(~ c("x1", "x2")) %>%
mutate(mu=abs(x1^3 - 30*sin(x2) + 10))
ggplot(dados.grid, aes(x=x1, y=x2)) +
geom_point(aes(colour=mu), size=2, shape=15) +
coord_cartesian(expand=F) +
scale_colour_gradient(low="white",
high="black",
name=TeX("$E(Y|X_1, X_2)$")) +
xlab(TeX("$X_1$")) + ylab(TeX("$X_2$"))
Figura 2: Arquitetura da rede neural artificial. Adotamos função de ativação sigmoide e linear nas camadas escondidas e de saída, respectivamente.
### Figura 2: Arquitetura da RNA.
par(mar=c(0, 0, 0, 0))
wts_in <- rep(1, 9)
struct <- c(2, 2, 1) # dois inputs, dois neurônios escondidos e um output
plotnet(wts_in, struct = struct,
x_names="", y_names="",
node_labs=F, rel_rsc=.7)
aux <- list(
x=c(-.8, -.8, 0, 0, .8, rep(-.55, 4), -.12, -0.06, .38, .38, .7),
y=c(.73, .28, .73, .28, .5, .78, .68, .48, .32, .88, .5, .68, .44, .7),
rotulo=c("x_1", "x_2", "h_1", "h_2", "\\hat{y}", "w_1", "w_3", "w_2", "w_4",
"b_1", "b_2", "w_5", "w_6", "b_3")
)
walk(transpose(aux), ~ text(.$x, .$y,
TeX(str_c("$", .$rotulo, "$")), cex=.8))
Considerando as informações acima, responda os itens a seguir.
Crie uma função computacional para calcular o valor previsto da variável resposta \(\hat{y}=f(\boldsymbol{x}; \boldsymbol{\phi})\) em função de \(\boldsymbol{x}\) e \(\boldsymbol{\Phi}\). Use a função para calcular \(\hat{y}\) para
\[\begin{equation*} \boldsymbol{\Phi}^\star = \left\{ \boldsymbol{\Omega} = \left\{ \boldsymbol{\Omega}_0 = \begin{pmatrix} 0.1 & 0.1 \\ 0.1 & 0.1 \end{pmatrix}, \boldsymbol{\Omega}_1 = \begin{pmatrix} 0.1 & 0.1 \end{pmatrix} \right\}, \boldsymbol{\beta} = \left\{ \boldsymbol{\beta}_0 = \begin{pmatrix} 0.1 \\ 0.1 \end{pmatrix}, \boldsymbol{\beta}_1 = 0.1 \right\} \right\} \; \text{e} \; \boldsymbol{x}=\begin{pmatrix} 2 \\ 1 \end{pmatrix}. \end{equation*}\]
Phi <- list(
Omega = list(
omega0 = matrix(c(.1,.1,
.1,.1),
2,2),
omega1 = matrix(c(.1,.1),
1,2)
),
Beta = list(
beta0 = matrix(c(.1,.1),
2,1),
beta1 = matrix(c(.1),1,1)
)
)
x <- matrix(c(2,1),
2,1)
mu <- abs(x[1]^3 - 30*sin(x[2]) + 10)
y <- rnorm(1, mean=mu, sd=1) # "Verdadeiro" valor.
ativacao <- list(
a = function(x){
return(1/(1+exp(-x)))
},
h = function(x){
return(x)
}
)
forward <- function(x, Phi, ativacao) {
f0 <- Phi$Omega$omega0 %*% x
f0 <- sweep(f0, 1, as.vector(Phi$Beta$beta0), "+") # Tive que fazer assim, pois a soma direta do vetor dava erro.
h1 <- ativacao$a(f0)
f1 <- Phi$Omega$omega1 %*% h1
f1 <- sweep(f1, 1, as.vector(Phi$Beta$beta1), "+")
y_hat <- ativacao$h(f1)
list(f0 = f0, h1 = h1, f1 = f1, y_hat = y_hat)
}
y_hat <- forward(x,Phi,ativacao)$y_hatO código acima implementa o exercício solicitado, e avalia o “modelo” em um ponto, obtida da previsão à partir dos valores dos parâmetros \(\boldsymbol{\Omega}\) de pesos e \(\boldsymbol{\beta}\) de viéses sugeridos, resultando em 0.22 — onde o valor gerado para \(y\) a partir da relação funcional
\[\begin{align*} Y & \sim N(\mu, \sigma^2=1) \\ \mu & = |X_1^3 - 30 \text{sen} (X_2) + 10| \\ X_j & \sim \text{Uniforme}(-3, 3), \quad j=1, 2, \end{align*}\]
foi 7.12, para esta seed.
Crie uma função computacional para calcular a função de perda \(J(\boldsymbol{\phi})\). Em seguida, divida o conjunto de dados observados de modo que as primeiras 80.000 amostras componham o conjunto de treinamento, as próximas 10.000 o de validação, e as últimas 10.000 o de teste. Qual é a perda da rede no conjunto de teste quando \(\boldsymbol{\phi}=\boldsymbol{\Phi}^\star\)?
mse <- function(y, y_hat) {
mean((y - y_hat)^2)
}x <- t(as.matrix(dados[, c("x1.obs", "x2.obs")]))
y <- matrix(dados$y, nrow = 1)
x_treino <- x[,1:8000]
x_validacao <- x[,8001:9000]
x_teste <- x[,9001:10000]
y_treino <- y[,1:8000]
y_validacao <- y[,8001:9000]
y_teste <- y[,9001:10000]y_hat_teste <- forward(x_teste,Phi,ativacao)$y_hatloss <- mse(y_teste, y_hat_teste)O erro quadrático médio recuperado do conjunto de teste, avaliando os dados na rede com \(\phi = \Phi^\star\) foi MSE = 673.29.
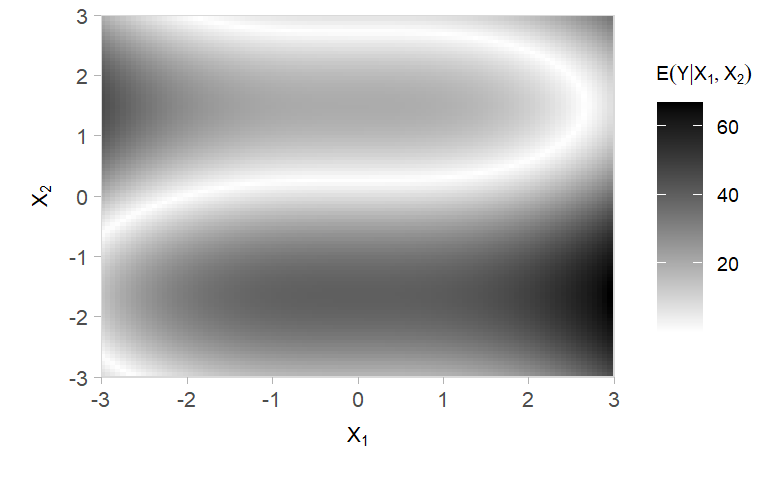
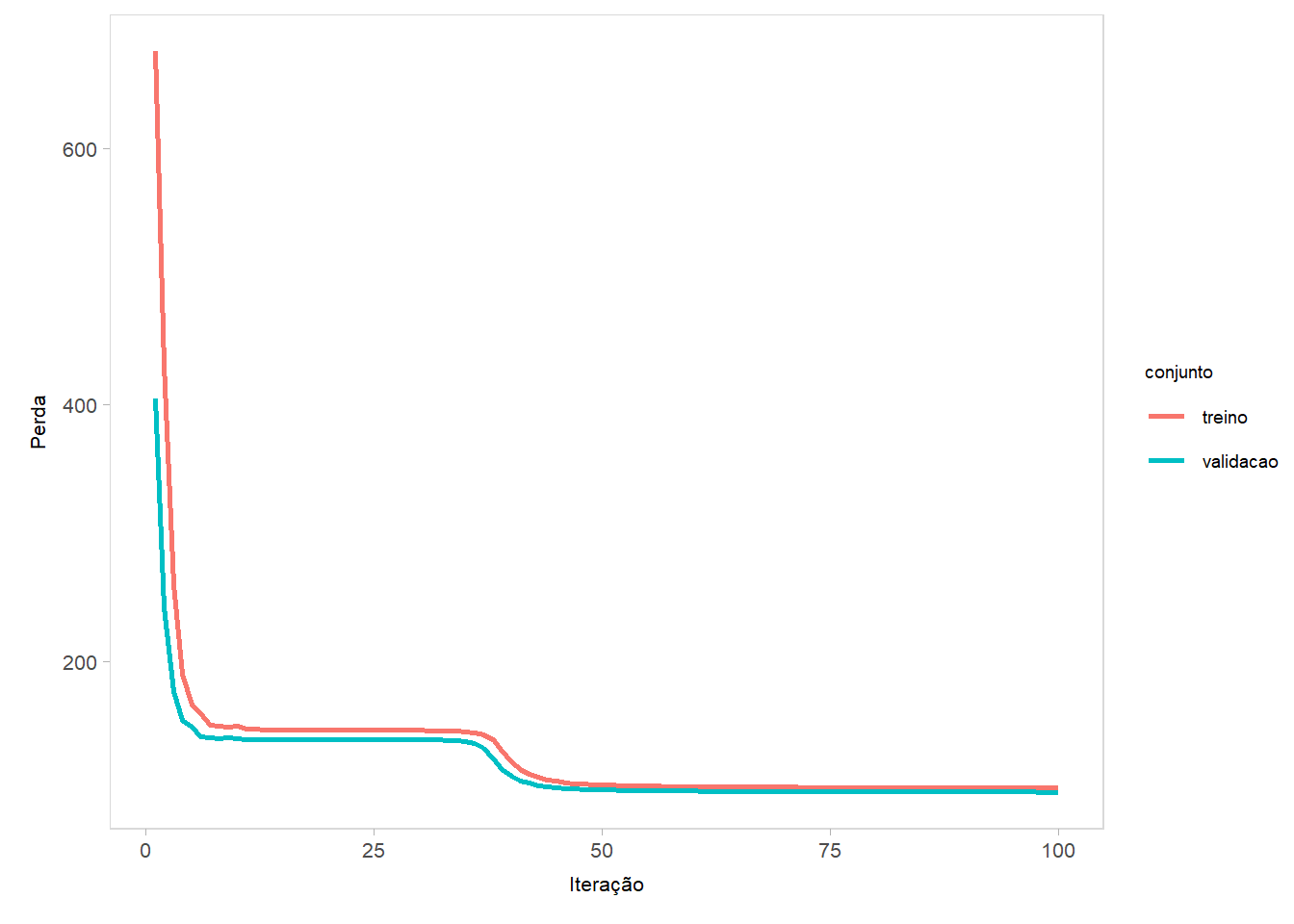
Use a regra da cadeia para encontrar expressões algébricas para o vetor gradiente \[ \nabla_{\boldsymbol{\phi}} J(\boldsymbol{\phi}) = \left(\frac{\partial J}{\partial w_1}, \ldots, \frac{\partial J}{\partial b_3} \right). \]
Temos que \(\frac{\partial J}{\partial \hat{y}_i}\) será a derivada da função de custo, no caso MSE, definido por \(J = \frac{1}{m}\sum^m_{i=1}(\hat{y}-y)^2\). Desta forma, para cada \(i\), \(\frac{\partial J}{\partial \hat{y}_i} = 2(\hat{y}_i-y_i)\); e para o conjunto de todos as \(i\) observações, \(\frac{\partial J}{\partial \hat{y}} = \frac{2}{m}\sum_{i=1}^m(\hat{y}_i-y_i)\). Como isso é um escalar, chamarei \(\frac{\partial J}{\partial \hat{y}_i}\) de \(\epsilon_{1,i}\) (e, consequentemente, \(\frac{\partial J}{\partial \hat{y}}\) de \(\epsilon_{1} = \frac{1}{m}\sum_{i=1}^m\epsilon_{1,i}\)).
Para encontrar \(\nabla_{\boldsymbol{\Phi}}J(\boldsymbol{\Phi}) = (\nabla_{\Omega_1}J, \nabla_{\beta_1}J,\nabla_{\Omega_0}J,\nabla_{\beta_0}J)\), devemos aplicar a regra da cadeia, e retropropagar as derivadas parciais, da seguinte forma:
Como \(\hat{y}_i = h(f_{1,i})\); e \(f_{1,i} = \boldsymbol{\Omega}_1\boldsymbol{h}_{1,i}+\beta_1\); e \(\boldsymbol{h}_{1,i} = a(\boldsymbol{f}_{0,i})\); e \(\boldsymbol{f}_{0,i} = \boldsymbol{\Omega}_0\boldsymbol{x}_i + \boldsymbol{\beta}_0\), temos que:
\[ \frac{\partial J}{\partial f_{1,i}} = \frac{\partial J}{\partial \hat{y}_i} \frac{\partial \hat{y}_i}{\partial f_{1,i}} = \epsilon_{1,i} * h'(f_{1,i}) = \epsilon_{1,i} * 1 = \epsilon_{1,i} \text{ (Visto que h(.) é função identidade)} \]
Aplicando a todas as \(i\) observações, teríamos que a perda total seria simplesmente
\[ \frac{\partial J}{\partial f_{1}} = \frac{1}{m}\sum_{i=1}^m\epsilon_{1,i} = \epsilon_1. \]
Como \(\boldsymbol{f}_{1,i}=\boldsymbol{\Omega}_1\boldsymbol{h}_{1,i} + \beta_1\), calculamos
\[ \frac{\partial\boldsymbol{f}_{1,i}}{\partial\boldsymbol{\Omega}_1} = \boldsymbol{h}_{1,i}^T \text{ (Visto que } \nabla_{\boldsymbol{f}} = \boldsymbol{J_f}^T \text{)}, \text{ e} \\ \frac{\partial\boldsymbol{f}_{1,i}}{\partial\beta_1} = 1. \]
Com estes resultados, podemos calcular
\[ \frac{\partial J}{\partial \boldsymbol{\Omega}_1} = \frac{\partial J}{\partial f_{1,i}} \frac{\partial f_{1,i}}{\partial \boldsymbol{\Omega}_1} = \frac{1}{m}\sum_{i=1}^m\epsilon_{1,i} * \boldsymbol{h}_{1,i}^T \text{, e} \]
\[ \frac{\partial J}{\partial \beta_1} = \frac{\partial J}{\partial \boldsymbol{f}_{1,i}} \frac{\partial \boldsymbol{f}_{1,i}}{\partial \beta_1} = \frac{1}{m}\sum_{i=1}^m\epsilon_{1,i} * 1. \]
Agora, para obtermos \(\frac{\partial J}{\partial \boldsymbol{\Omega}_0}\) e \(\frac{\partial J}{\partial \boldsymbol{\beta}_0}\), basta seguir retropropagando as derivadas parciais utilizando a regra da cadeia.
Como \(\boldsymbol{f}_{1,i} = \boldsymbol{\Omega}_1\boldsymbol{h}_{1,i}+\beta_1\), e \(\boldsymbol{h}_{1,i}=a(\boldsymbol{f}_{0,i})\), temos que:
\[ \frac{\partial J}{\partial \boldsymbol{f}_{0,i}} = \frac{\partial J}{\partial \boldsymbol{h}_{1,i}} \odot a'(\boldsymbol{f}_{0,i}), \]
onde \(a'(.)\) é a derivada da função sigmoide, escolhida como ativação para a camada oculta.
Derivando \(\frac{\partial \boldsymbol{f}_{1,i}}{\partial \boldsymbol{h}_{1,i}} = \nabla_{\boldsymbol{h}_{1,i}} (\boldsymbol{\Omega_1\boldsymbol{h}_{1,i}+\beta_1}) = \boldsymbol{\Omega}_1^T\). Então,
\[ \frac{\partial J}{\partial \boldsymbol{h}_{1,i}} = \frac{\partial J}{\partial \boldsymbol{f}_{1,i}} \frac{\partial \boldsymbol{f}_{1,i}}{\partial \boldsymbol{h}_{1,i}} = \epsilon_{1,i} * \boldsymbol{\Omega}_1^T, \]
para cada \(i\). De maneira análoga,
\[ \frac{\partial J}{\partial \boldsymbol{h}_{1}} = \frac{1}{m} \sum^m_{i=1} \epsilon_{1,i} * \boldsymbol{\Omega}_1^T. \]
E, desta forma,
\[ \frac{\partial J}{\partial \boldsymbol{f}_{0,i}} = (\epsilon_{1,i} * \boldsymbol{\Omega}_1^T) \odot a'(\boldsymbol{f}_{0,i}), \]
para cada \(i\). Então,
\[ \frac{\partial J}{\partial \boldsymbol{f}_{0}} = \frac{1}{m} \sum_{i=1}^m (\epsilon_{1,i} * \boldsymbol{\Omega}_1^T) \odot a'(\boldsymbol{f}_{0,i}), \]
será um vetor \(\nu_{(m_xp)}\). Desta forma, chamaremos \(\boldsymbol{\nu}_{0,i} = \frac{\partial J}{\partial \boldsymbol{f}_{0,i}} = (\epsilon_{1,i} * \boldsymbol{\Omega}_1^T) \odot a'(\boldsymbol{f}_{0,i})\), para cada \(i\).
Com estes resultados, podemos calcular diretamente os gradientes \(\frac{\partial J}{\partial \boldsymbol{\Omega}_0}\) e \(\frac{\partial J}{\partial \boldsymbol{\beta}_0}\), tal que:
\[ \frac{\partial J}{\partial \boldsymbol{\Omega}_0} = \frac{\partial J}{\partial \boldsymbol{f}_{0,i}} \frac{\partial \boldsymbol{f}_{0,i}}{\partial \boldsymbol{\Omega}_0} = \frac{1}{m}\sum_{i=1}^m\boldsymbol{\nu}_{0,i} * \boldsymbol{x}_i^T, \text{ e} \]
\[ \frac{\partial J}{\partial \boldsymbol{\beta}_0} = \frac{\partial J}{\partial \boldsymbol{f}_{0,i}} \frac{\partial \boldsymbol{f}_{0,i}}{\partial \boldsymbol{\beta}_0} = \frac{1}{m}\sum_{i=1}^m\boldsymbol{\nu}_{0,i} * 1 = \frac{1}{m}\sum_{i=1}^m\boldsymbol{\nu}_{0,i}. \]
Organizando então os resultados, temos
\[\begin{align*} \nabla_{\phi}J(\phi) &= (\nabla_{\Omega_1}J, \nabla_{\beta_1}J,\nabla_{\Omega_0}J,\nabla_{\beta_0}J) \\ &= \left( \epsilon_{1} \boldsymbol{h}_{1}^T, \epsilon_1, \boldsymbol{\nu}_0 \mathbf{x}^T, \boldsymbol{\nu}_0 \right). \end{align*}\]
Crie uma função computacional que receba como entrada a lista \(\boldsymbol{\Phi}\), uma matrix design (\(\boldsymbol{x}\)) e as respectivas observações (\(\boldsymbol{y}\)) e forneça, como saída, o gradiente definido no item c). Apresente o resultado da função aplicada sobre o banco de treinamento, quando \(\boldsymbol{\Phi}=\boldsymbol{\Phi}^\star\). Atenção: implemente o algoritmo back-propagation para evitar realizar a mesma operação múltiplas vezes.
a_linha <- function(x){
return(ativacao$a(x) * (1 - ativacao$a(x)) )
}
backprop <- function(x, y, Phi, fwd, ativacao) {
f0 <- fwd$f0
h1 <- fwd$h1
f1 <- fwd$f1
y_hat <- fwd$y_hat
m <- ncol(x)
delta1 <- 2 * (y_hat - y)
dOmega1 <- (1/m) * delta1 %*% t(h1)
dBeta1 <- (1/m) * matrix(rowSums(delta1))
delta0 <- (t(Phi$Omega$omega1) %*% delta1) * a_linha(f0)
dOmega0 <- (1/m) * delta0 %*% t(x)
dBeta0 <- (1/m) * matrix(rowSums(delta0), nrow = nrow(Phi$Beta$beta0))
list(dOmega0 = dOmega0, dBeta0 = dBeta0,
dOmega1 = dOmega1, dBeta1 = dBeta1)
}backprop(x_treino,y_treino,Phi,forward(x_treino,Phi,ativacao),ativacao)$dOmega0
x1.obs x2.obs
[1,] -0.2141997 0.6404715
[2,] -0.2141997 0.6404715
$dBeta0
[,1]
[1,] -1.072832
[2,] -1.072832
$dOmega1
[,1] [,2]
[1,] -22.36039 -22.36039
$dBeta1
[,1]
[1,] -43.39672Aplique o método do gradiente para encontrar os parâmetros que minimizam a função de perda no conjunto de treino. Inicie o algoritmo no ponto \[\begin{equation*} \boldsymbol{\Phi}^0 = \left\{ \boldsymbol{\Omega} = \left\{ \boldsymbol{\Omega}_0 = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}, \boldsymbol{\Omega}_1 = \begin{pmatrix} 0 & 0 \end{pmatrix} \right\}, \boldsymbol{\beta} = \left\{ \boldsymbol{\beta}_0 = \begin{pmatrix} 0 \\ 0 \end{pmatrix}, \boldsymbol{\beta}_1 = 0 \right\} \right\}, \end{equation*}\] use taxa de aprendizagem \(\epsilon=0.1\) e rode o algoritmo por 100 iterações. Para cada uma delas, calcule a perda no conjunto de validação. Apresente a lista de parâmetros estimados (isso é, aqueles que geraram a menor perda na validação), indique em qual iteração eles foram observados e comente o resultado.
Phi_zero <- list(
Omega = list(
omega0 = matrix(c(0,0,
0,0),
2,2),
omega1 = matrix(c(0,0),
1,2)
),
Beta = list(
beta0 = matrix(c(0,0),
2,1),
beta1 = matrix(c(0),1,1)
)
)update <- function(Phi, gradientes, learning_rate) {
Phi$Omega$omega0 <- Phi$Omega$omega0 - learning_rate * gradientes$dOmega0
Phi$Beta$beta0 <- Phi$Beta$beta0 - learning_rate * gradientes$dBeta0
Phi$Omega$omega1 <- Phi$Omega$omega1 - learning_rate * gradientes$dOmega1
Phi$Beta$beta1 <- Phi$Beta$beta1 - learning_rate * gradientes$dBeta1
return(Phi)
}train <- function(x_treino, y_treino, x_validacao, y_validacao, Phi, ativacao, learning_rate, epochs) {
losses_treino <- numeric(epochs)
losses_valid <- numeric(epochs)
melhor_valid <- Inf
melhor_Phi_valid <- Phi
melhor_epoch_valid <- 1
for (epoch in 1:epochs) {
fwd_treino <- forward(x_treino, Phi, ativacao)
loss_treino <- mse(y_treino, fwd_treino$y_hat)
gradientes <- backprop(x_treino, y_treino, Phi, fwd_treino, ativacao)
Phi <- update(Phi, gradientes, learning_rate)
fwd_valid <- forward(x_validacao, Phi, ativacao)
loss_valid <- mse(y_validacao, fwd_valid$y_hat)
losses_treino[epoch] <- loss_treino
losses_valid[epoch] <- loss_valid
if (loss_valid < melhor_valid) {
melhor_valid <- loss_valid
melhor_Phi_valid <- Phi
melhor_epoch_valid <- epoch
}
}
return(list(melhor_Phi_valid = melhor_Phi_valid,
menor_loss_valid = melhor_valid,
melhor_epoch_valid = melhor_epoch_valid,
losses_valid = losses_valid,
losses_treino = losses_treino))
}resultados <- train(x_treino, y_treino, x_validacao, y_validacao, Phi = Phi_zero, ativacao, learning_rate = 0.1, epochs = 100)resultados$melhor_Phi_valid$Omega
$Omega$omega0
x1.obs x2.obs
[1,] 1.329999 -5.605273
[2,] 1.329999 -5.605273
$Omega$omega1
[,1] [,2]
[1,] 10.60845 10.60845
$Beta
$Beta$beta0
[,1]
[1,] -3.029731
[2,] -3.029731
$Beta$beta1
[,1]
[1,] 13.16404A menor perda no conjunto de validação foi obtido na iteração 100. De fato, o algoritmo realiza o que se propõe — isto é:
Além disso, da forma que implementei a função, armazena as perdas nos conjuntos de treinamento e validação para cada iteração, e identifica em qual atualização a perda do conjunto de validação foi minimizada — salvando também o vetor de parâmetros \(\Phi\) e a perda correspondente à iteração.
Desta forma, poderíamos obter os melhores parâmetros \(\Phi\), definidos como aqueles que minimizam a perda no conjunto de validação, para testar a rede sobre o conjunto de teste, a fim de realizar a avaliação final da rede.
Como diagnóstico parcial, nota-se que o erro quadrático médio no conjunto de validação \(MSE_{validação}=\) 97.89 é um erro consideravelmente alto. Diversos fatores podem influenciar o fracasso da rede em obter um erro médio mais comportado, como:
Em suma, a rede funciona, mas ainda é muito inadequada para ser implementada em produção da forma que está.
Apresente o gráfico do custo no conjunto de treinamento e no de validação (uma linha para cada) em função do número da iteração do processo de otimização. Comente os resultados.
losses_df <- tibble(epoch = 1:100,
treino = resultados$losses_treino,
validacao = resultados$losses_valid) %>%
pivot_longer(cols = c(treino, validacao),
names_to = "conjunto",
values_to = "loss")
ggplot(losses_df) +
geom_line(
aes(x = epoch, y = loss, color = conjunto),
size = 1) +
labs(x = "Iteração", y = "Perda")
Pelo gráfico, podemos observar que tanto a perda no conjunto de treino quanto a perda no conjunto de validação seguiram trajetória descendente por praticamente todo o processo de otimização. Pode-se dizer que a rede não incorreu em overfitting; situação esta que seria praticamente impossível pelas características da rede (número fixo e reduzido de parâmetros em relação a massa de dados). Nota-se que houve uma grande diminuição da perda nas primeiras iterações, seguido de um platô por algumas iterações, até uma segunda trajetória descendente em torno da 35ª iteração, seguida posteriormente de outro platô até o final do processo de otimização. Pode-se dizer que o método do gradiente descendente foi capaz neste caso de ultrapassar um provável ponto de sela do espaço paramétrico e seguir trajetória descendente para um ponto inferior de gradiente, ainda que numa implementação simples sem utilizar métodos mais robustos como o Adam. Uma característica estranha é o fato da perda no conjunto de treino ter sido maior durante todo o processo, o que para uma perda definida como o erro quadrático médio, esperaria-se na maioria das situações que a perda do conjunto de validação fosse maior, visto que a otimização de fato ocorre no conjunto de treino. Isto provavelmente se deve pelo fato de ser uma rede simples e subparametrizada, onde o conjunto de treino — por ser maior — provavelmente contava com mais outliers, que inflaram sistematicamente a perda no processo.