XGBoost (eXtreme Gradient Boosting) (Tianqi Chen, 2016) é uma das implementações de three ensembling baseada em gradient boosting mais populares, por ser otimizado para desempenho e eficiência.
A ideia do algoritmo gradient boosting é realizar ensemble de M classificadores fracos para obter um modelo robusto que faça boas previsões. Estes classificadores serão árvores de decisão. Porém, diferentemente do AdaBoost estudado anteriormente, a regularização é feita a partir da minimização de uma função de perda diferenciável, e não pela atribuição de maior peso a instâncias classificadas erroneamente.
Introdução
Por se tratar de um modelo sequencial, em que a árvore \(i+2\) necessitará da informação dos resíduos da árvore \(i+1\), também herda a restrição de paralelismo que outros modelos de three ensembling também contém. Porém, a implementação do algoritmo XGBoost busca paralelizar todas as rotinas necessárias para construção do modelo, tornando sequencial apenas o início da construção de cada árvore.
graph LR
A[Dados] --> B[Modelo 1];
B --> C[Modelo 2];
C --> D[...];
D --> E[Modelo m];
E --> F[Ensembling dos modelos];
F --> G[Modelo final];
Gradient Boosting
O algoritmo base do XGBoost é o Gradient Boosting, no qual busca-se minimizar uma função de perda utilizando gradiente descendente. Esta otimização não será numérica, mas sim fornecida pela combinação das árvores geradas (boosting), que irão conduzir o gradiente para o mínimo global da função.
Cada um desses aprendizes fracos sequenciais irão focar nos resíduos da árvore anterior, buscando a divisão que minimize a função de perda definida (podendo ser default ou escolhida pelo usuário).
Gradient Boosting
Seja M o número de árvores fixadas para construção do modelo, o modelo final será dado pela fórmula \[F_M(x) = F_0(x) +\sum^M_{m=1}F_m(x)\] Em que \(F_M(x)\) será o modelo final para predições, \(F_0(x)\) será um modelo inicial de árvore, \(F_1(x)\) será o modelo que minimiza os resíduos do modelo \(F_0(x)\); \(F_2(x)\) será o modelo que minimiza os resíduos do modelo \(F_1(x)\), e assim por diante até o modelo \(F_{m}(x)\). Portanto, a classificação da i-ésima instância será dada por:\[\hat{y_i} = F_M(x_i)\]
Construção das árvores
Salvo a primeira árvore, que será um chute inicial, iremos definir uma função objetivo com sendo\[obj = \sum^n_{i=1}l(y_i,\hat{y}_i^{(t)})+\sum^t_{i=1}\Omega(f_i),\] em que o termo \(l(y_i,\hat{y}_i^{(t)})\) irá computar a perda relativa no t-ésimo passo, e \(\Omega(f_i)\) será o t-ésimo termo de regularização, e \(obj\) será baseado nos resíduos da árvore anterior.
O algoritmo escolhe a cada passo a árvore que minimiza \(obj\) com base nas features selecionadas automaticamente pelo modelo.
Under the hood
Para a seleção de features que irão minimizar a função objetivo, o algoritmo irá avaliar diversas possíveis divisões em diferentes features, construindo entre outras coisas histogramas para as features que ajudem a encontrar o melhor ponto de divisão. Para isso, o algoritmo utiliza do paralelismo, executando diversas divisões e encontrando a melhor possível de forma iterativa e rápida.
Desta forma, apesar de se tratar de um modelo sequencial, o algoritmo implementado utiliza em todas as etapas que for possível da computação paralelizada, afim de aproveitar ao máximo o desempenho computacional e retornar um modelo que seja robusto e rápido
Para maior aprofundamento teórico sobre o funcionamento do modelo, consulte XGBoost tutorial, seção 1.3
Flow do modelo
Uma forma simplificada de mostrar o funcionamento do XGBoost pode ser representada pelo seguinte grafo:
graph TD
A[Entrada de dados] --> B
B[Preparação dos Dados] --> B1 & B2 & B3
B1[Limpeza dos Dados]
B2[Normalização]
B3[Divisão Treino/Teste]
B1 & B2 & B3 --> B_Final[Dados Preparados]
B_Final --> C[Entrada de Dados no Modelo]
C --> D[Construção da Primeira Árvore]
D --> D1 & D2 & D3
D1[Avaliação das Divisões]
D2[Construção dos Nós]
D3[Combinação das Previsões]
D1 & D2 & D3 --> D_Final[Árvore Construída]
D_Final --> E[Entrada de Dados Residual para a Segunda Árvore]
E --> F[Construção da Segunda Árvore]
F --> F1 & F2 & F3
F1[Avaliação das Divisões]
F2[Construção dos Nós]
F3[Combinação das Previsões]
F1 & F2 & F3 --> F_Final[Segunda Árvore Construída]
F_Final --> G[Repetir o processo anterior m vezes]
G --> H[Avaliação do Modelo]
H --> I[Ensembling das Árvores com Pesos Relativos]
I --> J[Modelo final]
Não é necessário pré-processamento dos dados categóricos
Cada árvore reduz a perda comparada com a anterior
Random Permutations
Target Encoding
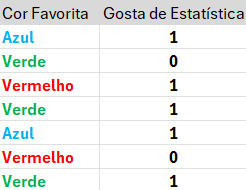
Target Encoding\[\frac {OptionCount+Prior}{n+1}\]
Prior: Palpite inicial arbitrário
Option Count: número de vezes que alguém da mesma cor gostou de estatística anteriormente
n: número de repetições da mesma cor já vistas
Processando variáveis categóricas
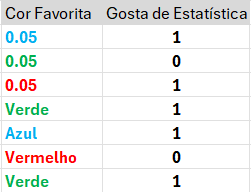
Target Encoding\[\frac {OptionCount+Prior}{n+1}\]
Target Encoding\[\frac {0+0.05}{0+1} = 0.05\]
Processando variáveis categóricas
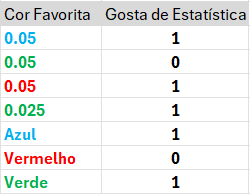
Target Encoding\[\frac {0+0.05}{1+1}\]
Target Encoding\[\frac {0.05}{2} = 0.025\]
Processando variáveis categóricas
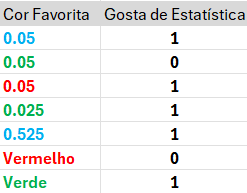
Target Encoding\[\frac {1+0.05}{1+1}\]
Target Encoding\[\frac {1.05}{2} = 0.525\]
Processando variáveis categóricas
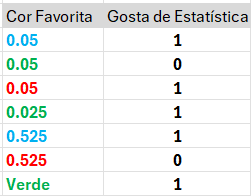
Target Encoding\[\frac {1+0.05}{1+1}\]
Target Encoding\[\frac {1.05}{2} = 0.525\]
Processando variáveis categóricas
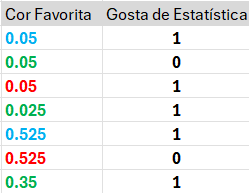
Target Encoding\[\frac {1+0.05}{2+1}\]
Target Encoding\[\frac {1.05}{3} = 0.35\]
Árvores de decisão Simétricas
Youtube: CatBoost Parte 2: Construindo e Usando Árvores
Gera modelos mais fracos, porém mais simples
Gera previsões mais rapidamente
Flow do modelo CatBoost
Uma forma simplificada de mostrar o funcionamento do Catboost pode ser representada pelo seguinte grafo:
graph TD
A[Entrada de dados] --> B
B[Preparação dos Dados] --> B1 & B3
B1[Limpeza dos Dados]
B3[Divisão Treino/Teste]
B1 & B3 --> B_Final[Dados Preparados]
B_Final --> C[Entrada de Dados no Modelo]
C[Entrada de Dados no Modelo] --> K1[Random Permutations]
K1[Random Permutations] --> K2[Target Encoding]
K2[Target Encoding] --> D[Construção da Primeira Árvore]
D --> D1 & D2 & D3
D1[Avaliação das Divisões]
D2[Construção dos Nós]
D3[Combinação das Previsões]
D1 & D2 & D3 --> D_Final[Árvore Construída]
D_Final --> E[Entrada de Dados Residual para a Segunda Árvore]
E --> F[Construção da Segunda Árvore]
F --> F1 & F2 & F3
F1[Avaliação das Divisões]
F2[Construção dos Nós]
F3[Combinação das Previsões]
F1 & F2 & F3 --> F_Final[Segunda Árvore Construída]
F_Final --> G[Repetir o processo anterior m vezes]
G --> H[Avaliação do Modelo]
H --> I[Ensembling das Árvores com Pesos Relativos]
I --> J[Modelo final]
