Modelo de regressão Birnbaum-Saunders reparametrizado pela média

Modelos Lineares Generalizados

Bruno Gondim Toledo

Introdução

A distribuição Birnbaum-Saunders (Birnbaum and Saunders, 1969) é utilizada para descrever tempo de vida por fadiga (exposição cumulativa a danos, vibrações, etc) de materiais expostos à ciclos homogêneos. O processo de fadiga descrito pelos autores é:

  • Um material sujeito a ciclo de cargas repetitivos, que produzem desgaste no material;
  • A falha no material dar-se-á quando a magnitude do desgaste excede um limite \(\omega\);
  • Os ciclos são homogêneos (a sequência de estresse aplicada ao material é sempre a mesma);
  • A extensão da fissura (\(X_i\)) causada pela carga \(l_i\) é uma variável aleatória com dependência nas cargas e fissuras acumuladas até o i-ésimo ciclo;
  • O tamanho total da fissura causados no j-ésimo ciclo (\(Y_j\)) também é uma variável aleatória com média \(\mu\) e variância \(\sigma^2 < \infty\);
  • O tamanho das fissuras \(Y_j\) em diferentes ciclos são independentes.

A distribuição Birnbaum-Saunders

Para este problema, os autores definem que: Seja T o tempo total até a ocorrência da falha e cumprida as condições de regularidade, podemos dizer que T segue distribuição Birnbaum-Saunders (BS), tal que \(T \sim BS(\alpha,\beta)\), e \[T = \beta\biggl(\frac{\alpha}{2}Z+\sqrt{(\frac{\alpha}{2}Z)^2+1} \biggl),\] onde \(\alpha\) é um parâmetro de forma, \(\beta\) é parâmetro de localização (mediana), e \(Z\) é uma variável aleatória com distribuição normal padrão.

Em uma aplicação, os parâmetros \(\alpha\) e \(\beta\) devem ser estimados.

Reparametrização da Birnbaum-Saunders

Em geral, iremos trabalhar com uma reparametrização da distribuição Birnbaum-Saunders, especialmente para regressão. Rieck e Nedelman (1991) mostram a relação da distribuição Birnbaum-Saunders com a distribuição seno hiperbólico normal.

Seja \(T \sim BS(\alpha,\beta)\), então \(Y \sim SHN(\alpha,log(\beta),\sigma=2)\), onde \(\alpha\) é parâmetro de forma, \(\beta\) é parâmetro de localização, e \(\sigma\) é parâmetro de de escala fixo.

Desta forma, a distribuição seno hiperbólica normal pode também ser chamada de distribuição log-Birnbaum-Saunders (LBS).

Regressão Birnbaum-Saunders

Assumindo \(T_i\) variável resposta, podemos construir um modelo de regressão Birbaum-Saunders, tal que: \[T_i = \beta_i\varphi_i = exp(\mu_i)\varphi_i=exp(\mathbf{x}_i^T\mathbf{\eta})\varphi_i, i = 1,2,...,n.\] onde \(T_i\) e \(\beta_i = exp(\mu_i)\) são a variável resposta e a mediana para a i-ésima observação; \(\mathbf{\eta} = (\eta_0,\eta_1,...,\eta_p)^T\) é o vetor de parâmetros desconhecidos a serem estimados pela regressão, \(\mathbf{x}_i^T=(1,x_{i1},...,x_{ip})\) são os valores das \(p\) variáveis explicativas, e \(\varphi_i \sim BS(\alpha,1)\) é o erro do modelo, tal que \(T_i \sim BS(\alpha,\beta)\).

Função de verossimilhança

Para construir a função de verossimilhança, será necessário reparametrizar a distribuição \(T_i \sim BS(\alpha,\beta_i)\) para \(Y_i = log(T_i) \sim LBS(\alpha,log(\beta_i))\), tal que \[log(T_i) = Y_i = \mu_i + \epsilon_i = \mathbf{x}_i^T\mathbf{\eta}+\epsilon_i, i=1,...,n.\]

Desta forma, a função de verossimilhança para \(\mathbf{\theta}=(\alpha,\mathbf{\eta}^T)^T\) não terá solução analítica, sendo necessário estimar o vetor de parâmetros \(\mathbf{\eta}\) utilizando métodos iterativos de otimização não linear.

Desta estimativa obtida, podemos obter a estimativa de máxima verossimilhança do parâmetro \(\alpha\), tal que: \[\hat{\alpha} = \sqrt{\frac{4}{n}\sum_{i=1}^nsinh^2\biggl(\frac{y_i-\mathbf{x}_i^T\mathbf{\hat{\eta}}}{2}\biggl)}.\]

Estimador de mínimos quadrados

Podemos também utilizar o estimador de mínimos quadrados para \(\mathbf{\eta}\), da forma \[\hat{\mathbf{\eta}}=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y},\] onde \(\mathbf{y}\) é o vetor de observações, e \(\mathbf{X}\) é a matriz de desenho do modelo. Entretanto, este método é menos eficiente que o estimador de máxima verossimilhança, conforme observado por Rieck e Nedelman (1991).

Distribuição BS reparametrizada pela média

Santos-Neto et al. (2012) propuseram uma reparametrização da distribuição Birnbaum-Saunders, sendo: \(\alpha=\frac{2}{\delta},\beta=\frac{\delta\mu}{\delta+1},\) tal que \(\delta=\frac{2}{\alpha^2},\mu=\beta\Bigl(1+\frac{\alpha^2}{2}\Bigl)\), sendo \(\delta>0,\mu>0\) parâmetros de forma e média, respectivamente.

Nesta parametrização, a função de densidade de probabilidade fica definida por: \[f_Y(y|\mu,\delta)=\frac{exp(\frac{\delta}{2}\sqrt{\delta+1})}{\sqrt{16\pi\mu}y^{\frac{3}{2}}}\Bigl(y+\frac{\delta\mu}{\delta+1}\Bigl)exp\Biggl(-\frac{\delta}{4}\Biggl[\frac{y(\delta+1)}{\delta\mu}+\frac{\delta\mu}{y(\delta+1)}\Biggl]\Biggl)\]

Regressão BS reparametrizada pela média

Sendo \(RBS(\mu,\delta)\) a reparametrização pela média da distribuição Birnbaum-Saunders original, Leiva et al. (2014) propõe um modelo de regressão em que, seja \(Y \sim RBS(\mu,\delta)\), a média de \(Y_i\) satisfaz a relação: \[h(\mu_i)=\mathbf{x}_i^T\mathbf{\beta}, i=1,...,n,\] em que \(\mathbf{\beta}=(\beta_1,...,\beta_p)^T,p<n\) é vetor de coeficientes de regressão a serem estimados, e \(\mathbf{x}_i=(x_{i1},x_{i2},...,x_{ip})^T\) são observações de p regressores, e \(\mu_i=h^{-1}(\mathbf{x}_i^T\mathbf{\beta}),\) com \(h(.)\) sendo uma função de ligação positiva e duas vezes diferenciável.

Sob a distribuição RBS, \(\mathbb{E}(Y)=\mu\) e \(Var(Y) = \mu^2 CV(Y)^2\), onde \(CV(Y) = \frac{\sqrt{2\delta+5}}{(\delta+1)}\in (0,\sqrt{5})\) é o coeficiente de variação de Y.

A variância de \(Y_i\) é função de \(\mu_i\), logo estaremos modelando também a variância.

Vantagens e desvantagens dos modelos BS

Vantagens

  • Mais uma família para obter um ajuste melhor aos dados;

  • Pode ser utilizada para dados censurados;

  • Resultados do modelo têm interpretação fácil;

  • Implementado no R!

Desvantagens

  • Distribuição pouco conhecida;

  • Limitações conceituais e práticas;

  • Definição matemática complexa;

  • Pouco material prático disponível de forma fácil.

Aplicação

Utilizarei o conjunto de dados cpd do pacote faraway, referente a projeção de vendas e o verdadeiro número de vendas de 20 produtos

library(tidyverse)
library(gamlss)
data(cpd,package='faraway')
attach(cpd)
p1 = cpd %>% 
  gather() %>%
  ggplot(aes(value)) +
  geom_histogram(bins = 30) +
  facet_wrap(~key, scales = 'free_x') +
  labs(x = '', y = '', title = '') +
  theme_minimal()

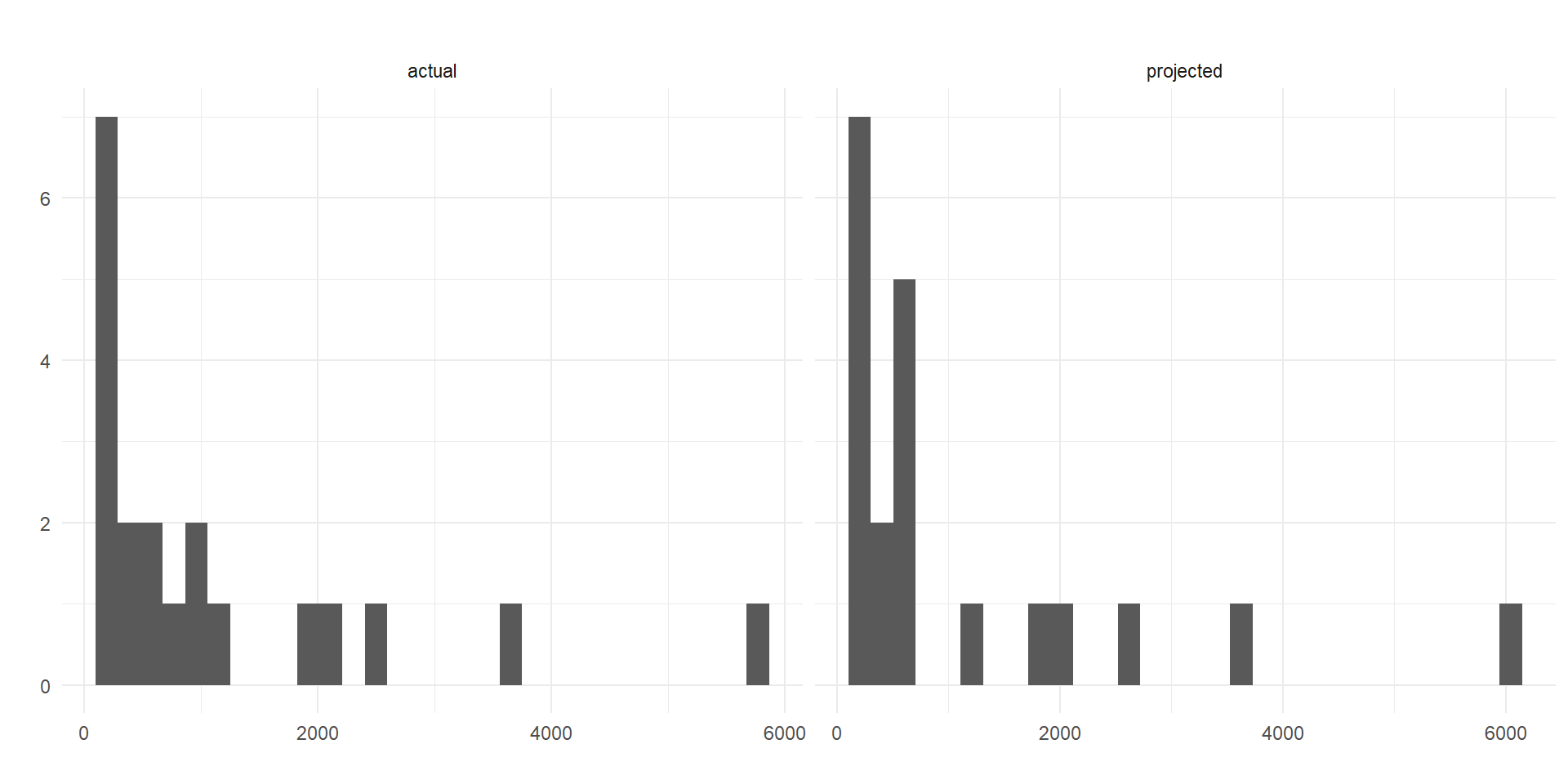
Vemos que tanto a variável resposta, actual, quanto a covariável explicativa, projected, são obviamente positivas, e também assimétricas à direta.

Primeiro ajuste

Veremos qual distribuição o pacote gamlss recomenda para melhor ajuste aos dados

mod = fitDist(actual, type="realplus") 
mod$fits
      IG     BCPE   IGAMMA   LOGNO2    LOGNO      GIG       GG    BCCGo 
319.7223 320.9136 320.9552 321.5667 321.5667 321.7220 322.8726 323.0453 
    BCCG      EXP  PARETO2       GP PARETO2o      GB2      WEI     WEI2 
323.0453 323.5004 324.1676 324.1676 324.1676 324.8727 324.9636 324.9636 
    WEI3     BCTo       GA   exGAUS 
324.9636 325.0453 325.3356 352.5137

Vemos que o pacote GAMLSS oferece diversas opções de ajuste para este conjunto de dados. Entretanto, estamos especialmente interessados em tentar ajustar os dados utilizando o modelo RBS

Ajuste RBS

Primeiramente, é necessário baixar e instalar o pacote RBS, que não está disponível no CRAN, utilizando o comando

devtools::install_github("santosneto/RBS")
library(RBS)

Agora, tentaremos o ajuste utilizando a distribuição RBS, e aproveitando da sintaxe e funcionalidades do pacote gamlss

Ajustando o modelo

model0 = gamlss::gamlss(actual ~ projected, family=RBS(mu.link="identity"),method=CG())
summary(model0)
******************************************************************
Family:  c("RBS", "BirnbaumSaunders") 

Call:  
gamlss::gamlss(formula = actual ~ projected, family = RBS(mu.link = "identity"),  
    method = CG()) 

Fitting method: CG() 

------------------------------------------------------------------
Mu link function:  identity
Mu Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.80360   18.08128   0.155    0.879    
projected    1.08047    0.07339  14.722 4.16e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

------------------------------------------------------------------
Sigma link function:  log
Sigma Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   3.9020     0.3162   12.34 6.56e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

------------------------------------------------------------------
No. of observations in the fit:  20 
Degrees of Freedom for the fit:  3
      Residual Deg. of Freedom:  17 
                      at cycle:  8 
 
Global Deviance:     247.755 
            AIC:     253.755 
            SBC:     256.7422 
******************************************************************

Modelando também a variância

model = gamlss::gamlss(actual ~ projected, sigma.formula = ~projected, family=RBS(mu.link="identity"),method=CG())
summary(model)
******************************************************************
Family:  c("RBS", "BirnbaumSaunders") 

Call:  
gamlss::gamlss(formula = actual ~ projected, sigma.formula = ~projected,  
    family = RBS(mu.link = "identity"), method = CG()) 

Fitting method: CG() 

------------------------------------------------------------------
Mu link function:  identity
Mu Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 34.81320   21.00592   1.657    0.117    
projected    0.95759    0.01903  50.318   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

------------------------------------------------------------------
Sigma link function:  log
Sigma Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 3.1348243  0.4749559   6.600  6.1e-06 ***
projected   0.0010326  0.0003238   3.189   0.0057 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

------------------------------------------------------------------
No. of observations in the fit:  20 
Degrees of Freedom for the fit:  4
      Residual Deg. of Freedom:  16 
                      at cycle:  20 
 
Global Deviance:     241.0335 
            AIC:     249.0335 
            SBC:     253.0165 
******************************************************************

Diagnósticos

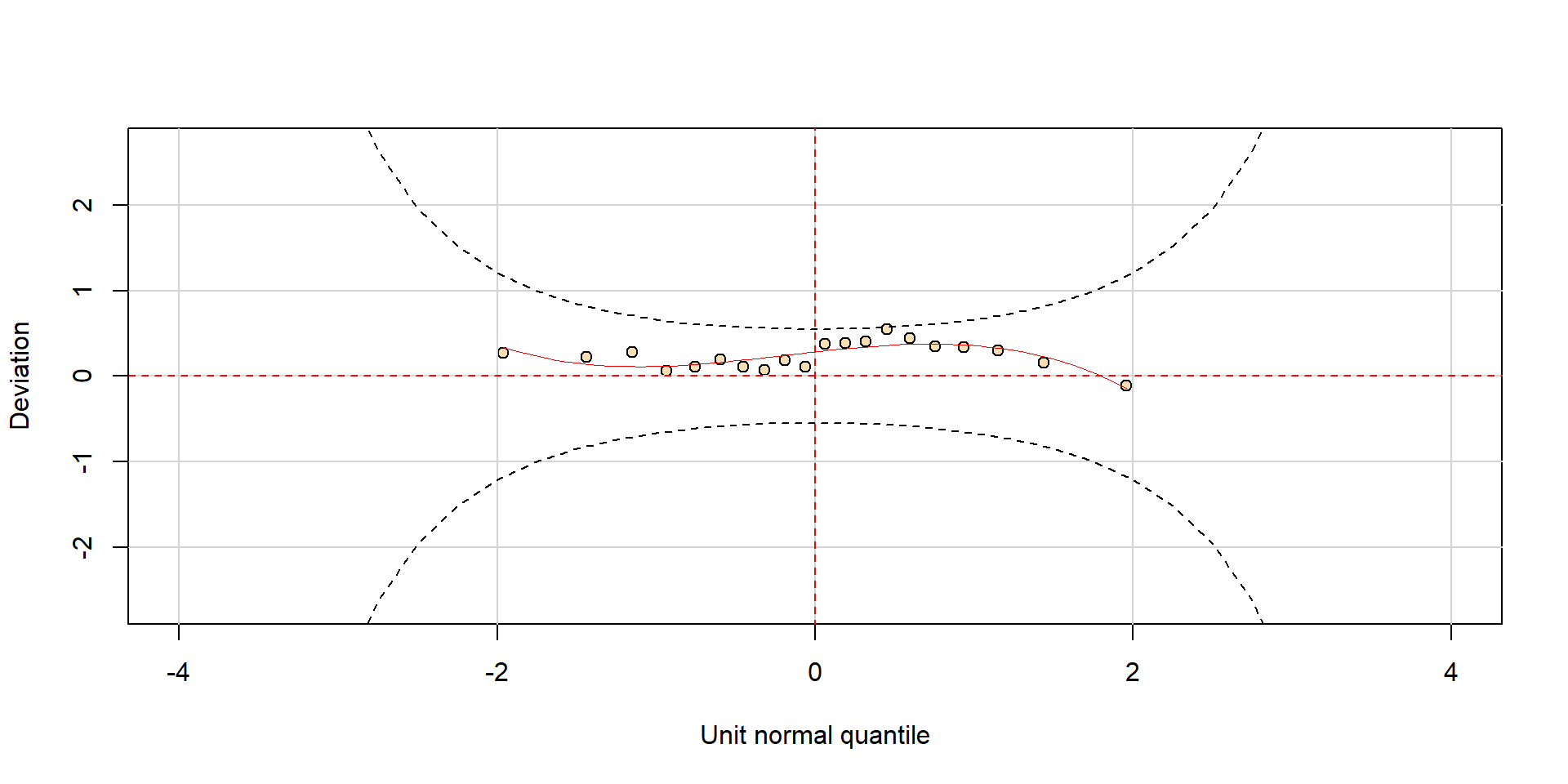
Podemos realizar a rotina normal de análise de diagnósticos do modelo, utilizando as funcionalidades do pacote gamlss

wp(model)

plot(model)

******************************************************************
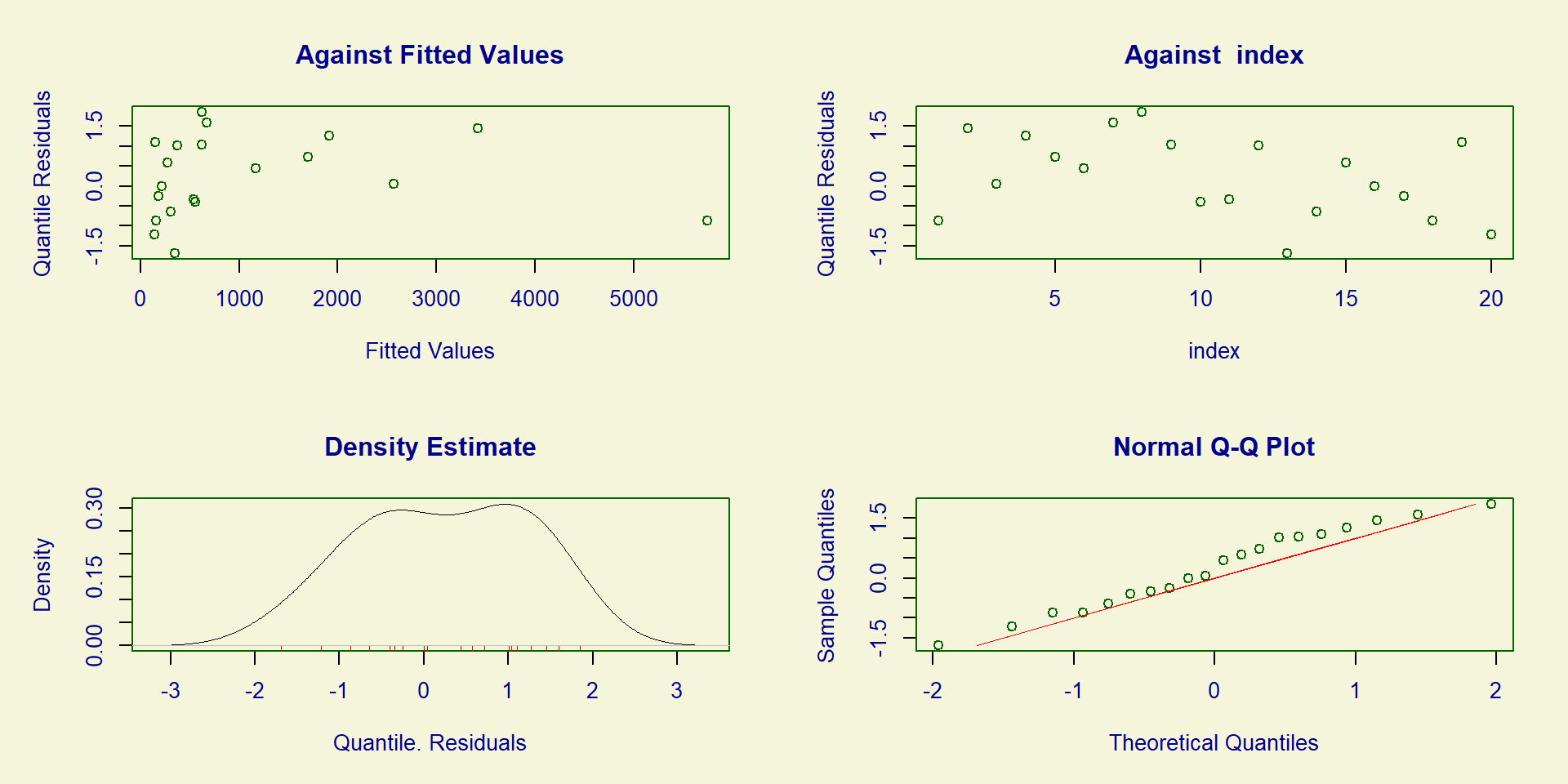
          Summary of the Quantile Residuals
                           mean   =  0.2395729 
                       variance   =  1.024173 
               coef. of skewness  =  -0.1452511 
               coef. of kurtosis  =  1.76144 
Filliben correlation coefficient  =  0.9877058 
******************************************************************

Referências

Birnbaum, Z. and Saunders, S. (1969). A new family of life distributions. Journal of Applied Probability, 6:319–327.

Santos-Neto, M., Cysneiros, F., Leiva, V., and Ahmed, S. (2012). On new parameterizations of the Birnbaum-Saunders distribution. Pakistan Journal of Statistics, 28:1–26.

Santos-Neto, M., Cysneiros, F., Leiva, V., and Barros, M. (2014). On new parameterizations of the Birnbaum-Saunders distribution and its moments, estimation and application. Revstat Statistical Journal, 12:247–272.

Leiva, V., Santos-Neto, M., Cysneiros, F., and Barros, M. (2014). BirnbaumSaunders statistical modelling: a new approach. Statistical Modelling, 14:21–48.

Rieck, J. and Nedelman, J. (1991). A log-linear model for the Birnbaum-Saunders distribution. Technometrics, 3:51–60.

Notas de aula do Prof. Helton Saulo. Disciplina Tópicos em Estatística 2 — Modelagem com apoio computacional. UnB, 2º/2024.