graph TD
A[Recebimento] --> B{Triagem Inicial};
B --> C[Distribuição];
B --> T1[...];
T1 --> T2[Busca por similaridade com \n outros processos do acervo];
T2 --> T3[...];
T3 --> B;
C --> D[...];
Similaridade de Processos Judiciários Utilizando Processamento de Linguagem Natural
Estudante
Orientadora
Sumário
Introdução
Conjunto de dados
Referencial teórico
Resultados
Conclusão
Referências
Introdução
O Ministro Luís Roberto Barroso assumiu a presidência do Tribunal em 2023, e estipulou como uma de suas metas de gestão a diminuição do acervo de processos de controle concentrado em 20%.
A tarefa de busca de processos similares no acervo de controle concentrado é feita hoje manualmente. Portanto, a identificação automatizada possibilita reduzir o tempo e o esforço manual na busca de processos similares.
Nesse trabalho, buscou-se aplicar técnicas de processamento de linguagem natural (NLP) para detecção de processos semelhantes no acervo de processos de controle concentrado do Tribunal.
Conjunto de dados
Os dados utilizados para esta análise são as petições iniciais dos processos de controle concentrado. Este é o primeiro documento que chega no Tribunal tratando de um processo.
Desta forma, o desafio é encontrar similaridades entre processos na sua fase inicial de tramitação, tal que esta ferramenta seja desbravadora na busca de similaridades antes de outros encaminhamentos internos no Tribunal.
As petições iniciais são um dado público, e podem ser obtidas no Portal do STF.
Para realizar a busca por similaridades, necessitamos fixar um processo, que chamaremos de paradigma.
Os processos paradigmas selecionados foram aqueles que tiveram pauta ou decisão conjunta pelo Tribunal com outros processos.
Desta forma, buscou-se encontrar técnicas que apontassem a similaridade desses processos já em suas petições iniciais.
Referencial teórico — Vetorização
Por se tratar de um dado textual, é necessário aplicar técnicas de vetorização ao texto.
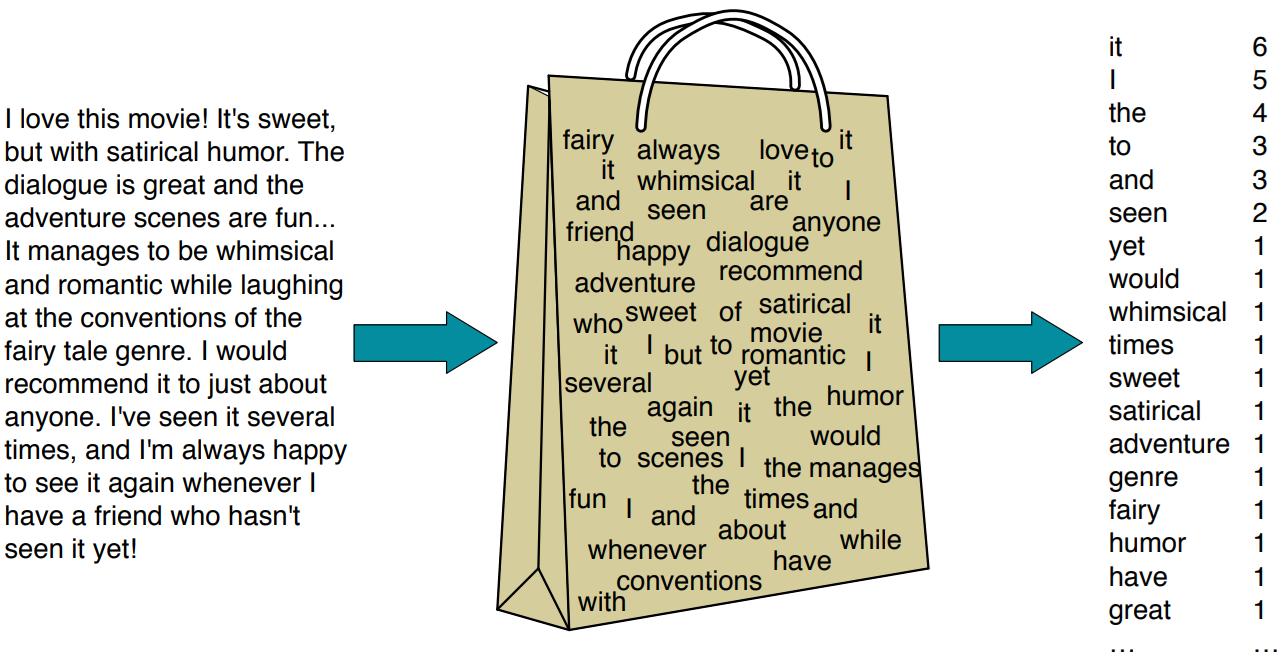
Esta é uma das formas mais simples de vetorizar um texto. Iremos simplesmente tabelar a frequência de utilização de cada um dos termos presentes no texto.
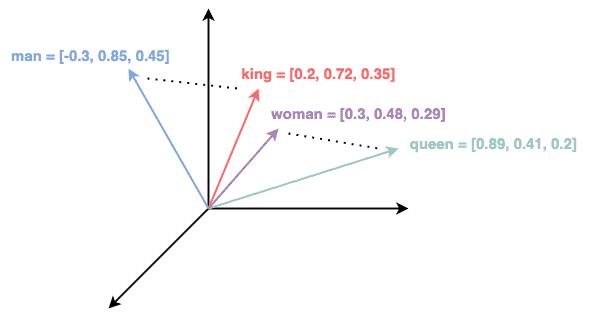
Esta é uma das formas mais sofisticadas para vetorização de texto. Nela, iremos obter o vetor numérico que representa o texto pelo treinamento de uma rede neural. Os parâmetros deste modelo são atualizados buscando prever a próxima palavra dado o seu contexto e dado um vetor de palavras que formam coletivamente o texto (Freitas et al. ,2024).
Referencial teórico — Métricas de similaridade
Para comparar os vetores criados, necessitamos de métricas de distância estatística
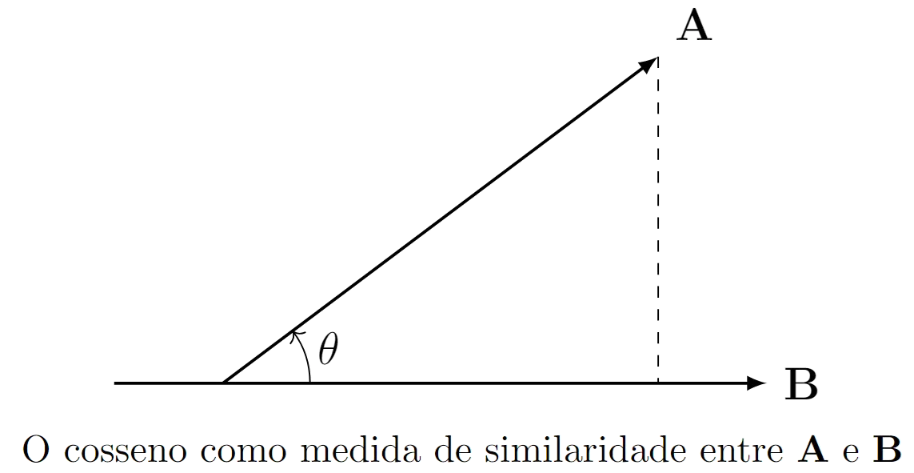
Pela Lei dos cossenos:
\[\begin{equation} \mathbf{A} \cdot \mathbf{B} = | \mathbf{A}|| \mathbf{B}|\cos\theta. \end{equation}\]
Podemos utilizar, para avaliar o grau de similaridade entre os vetores \(\mathbf{A}\) e \(\mathbf{B}\), a correlação entre eles. E para quantificar esta correlação, podemos utilizar o cosseno do ângulo entre estes vetores, tal que:
\[\begin{equation}\text{sim}(\mathbf{A,B}) = \cos\theta = \frac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{A}|| \mathbf{B}|}. \end{equation}\]
Esta é possivelmente a métrica mais utilizada no paradigma de NLP.
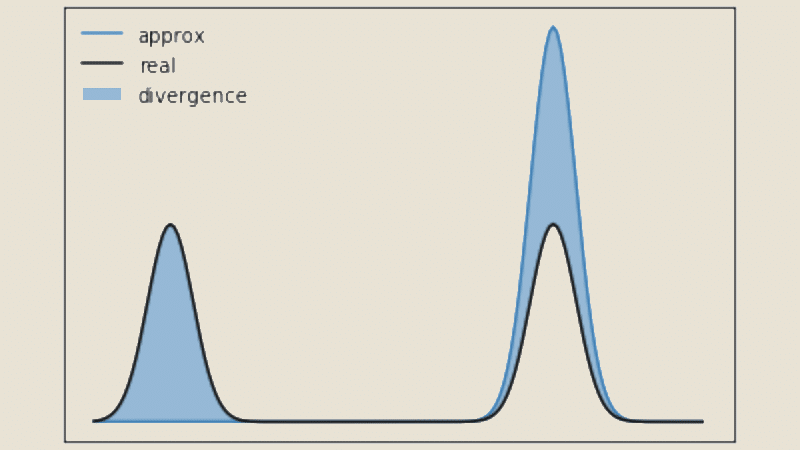
Uma outra métrica popular na área de Machine Learning, podemos calcular o complementar da divergência de Jensen-Shannon definida por:
\[\begin{equation} JSD(P||Q) = \\ \frac{1}{2}(KL(P||R)+KL(Q||R)), \end{equation}\]
como sendo uma medida de similaridade entre duas distribuições de probabilidade. No caso, tomamos os vetores como distribuições de probabilidade empírica. Esta é uma alternativa interessante a distância do cosseno, visto que esta métrica respeita a desigualdade triangular.
Referencial teórico — IMPE
Uma terceira métrica foi proposta para a medição da similaridade entre os processos, a qual se chamou Interseção mínima de probabilidade empírica (IMPE).
Esta métrica foi construída inspirada no índice de Tversky.
Nela, consideraremos os vetores dos textos como distribuições de probabilidade empírica. Destes, tomaremos um menos a soma das diferenças dos absolutos das frequência relativa de um termo entre dois textos, tal que \[\begin{equation} \text{IMPE}(\textbf{A},\textbf{B}) = 1 - \sum_{w \in A \cap B} |f_A(w) - f_B(w)|. \end{equation}\]
Por somar os menores valores, esta métrica foi construída para ser conservadora, apenas acusando similaridade entre textos muito parecidos.
\(IMPE(\textbf{A},\textbf{B}) \in (0,1)\), em que \(IMPE(\textbf{A},\textbf{B}) = 1 \rightarrow\) textos idênticos.
# Calcular interseção mínima de probabilidade empírica entre dois documentos ----
# Entrada: 2 df n x 2, coluna 1 "word" coluna 2 "freq"
IMPE <- function(df1, df2) {
df1$relative_freq <- df1$freq / sum(df1$freq)
df2$relative_freq <- df2$freq / sum(df2$freq)
common_words <- merge(df1, df2, by = "word", suffixes = c("_df1", "_df2"))
common_words$dissimilaridade <- abs(common_words$relative_freq_df1 - common_words$relative_freq_df2)
similaridade <- 1 - sum(common_words$dissimilaridade)
return(similaridade)
}Resultados
Foram realizados estudos de casos, onde se comparou a combinação de cada técnica de vetorização com cada métrica de similaridade para casos onde se sabia os processos que deveriam ser identificados como mais parecidos. Estes foram os resultados:
| Vetorização | Métrica de similaridade | Proximidade |
|---|---|---|
| doc2vec | Distância do cosseno | 8º mais similar |
| Bag of Words completo | Distância do cosseno | 1º mais similar |
| IMPE | 65º mais similar | |
| Jensen-Shannon | 3º mais similar | |
| Bag of Words reduzido | Distância do cosseno | 7º mais similar |
| IMPE | 4º mais similar | |
| Jensen-Shannon | 72º mais similar |
| Vetorização | Métrica de similaridade | Proximidade |
|---|---|---|
| doc2vec | Distância do cosseno | 1º e 2º mais similar |
| Bag of Words completo | Distância do cosseno | 1º e 2º mais similar |
| IMPE | 42º e 89º mais similar | |
| Jensen-Shannon | 1º e 3º mais similar | |
| Bag of Words reduzido | Distância do cosseno | 1º e 2º mais similar |
| IMPE | 8º e 9º mais similar | |
| Jensen-Shannon | 1º e 2º mais similar |
| Vetorização | Métrica de similaridade | Proximidade |
|---|---|---|
| doc2vec | Distância do cosseno | 4º mais similar |
| Bag of Words completo | Distância do cosseno | 1º mais similar |
| IMPE | 36º mais similar | |
| Jensen-Shannon | 3º mais similar | |
| Bag of Words reduzido | Distância do cosseno | 1º mais similar |
| IMPE | 8º mais similar | |
| Jensen-Shannon | 2º mais similar |
| Vetorização | Métrica de similaridade | Proximidade |
|---|---|---|
| doc2vec | Distância do cosseno | 1º e 6º mais similar |
| Bag of Words completo | Distância do cosseno | 1º e 2º mais similar |
| IMPE | 437º e 475º mais similar | |
| Jensen-Shannon | 1º e 2º mais similar | |
| Bag of Words reduzido | Distância do cosseno | 1º e 2º mais similar |
| IMPE | 3º e 4º mais similar | |
| Jensen-Shannon | 1º e 2º mais similar |
| Vetorização | Métrica de similaridade | Proximidade |
|---|---|---|
| doc2vec | Distância do cosseno | 1º e 5º mais similar |
| Bag of Words completo | Distância do cosseno | 3º e 4º mais similar |
| IMPE | 358º e 360º mais similar | |
| Jensen-Shannon | 2º e 3º mais similar | |
| Bag of Words reduzido | Distância do cosseno | 2º e 3º mais similar |
| IMPE | 6º e 7º mais similar | |
| Jensen-Shannon | 2º e 4º mais similar |
Resultados — t-SNE
Testou-se utilizar t-SNE para visualização do acervo, com objetivo de que as semelhanças entre processos fossem preservadas
Teste 1

Teste 2

Teste 3

Como os resultados não foram satisfatórios, esta técnica não foi utilizada na aplicação final.
Conclusão
A combinação das técnicas mais simples de vetorização Bag of Words com a distância do cosseno produziu excelentes resultados na busca de similaridade de processos.
Este resultado mostra que técnicas simples e parcimoniosas ainda são úteis para problemas práticos no paradigma da NLP.
A implementação de um aplicativo Shiny para utilização deste modelo fornece um valioso insumo para os analistas do Tribunal para o cumprimento da meta de diminuição do acervo de processos de controle concentrado do Ministro Presidente do STF.
Referências
FREITAS, L. J. G. Clusterização de textos aplicada ao tratamento de dados jurídicos desbalanceados. Tese (Mestrado em Estatística) – Departamento de estatística, Universidade de Brasília, 2023.
FREITAS, L. J. G.; ALENCAR, E.; RODRIGUES, T. C. V. Rafa 2030-deep learning applied to brazilian supreme court legal documents and un 2030 agenda. Galoá, 2022.
FREITAS, L. J. G. et al. Catboost algorithm application in legal texts and un 2030 agenda. Revista de Informatica Teórica e Aplicada - RITA - ISSN 2175-2745. Vol. 30, Num. 02 (2023) 51-58, 2023.
FREITAS, L. J. G. et al. Text clustering applied to data augmentation in legal contexts. arXiv preprint arXiv:2404.08683, 2024.
LU, J.; HENCHION, M.; NAMEE, B. M. Diverging divergences: Examining variants of jensen shannon divergence for corpus comparison tasks. 2021.
MORETTIN, P. A.; SINGER, J. M. Estatística e Ciência de Dados. 1ª. ed. Rio de Janeiro: LTC, 2023.
SOARES, A. Introdção à análise textual aplicada à sociologia. 2022. Disponível em: ⟨https://soaresalisson.github.io/analisetextual/⟩. Acesso em: 31 de dez. de 2024.

Departamento de estatística - UnB